Struktura, vlastnosti a změny skupenství pevných látek

Pevné látky

a) krystalické – pravidelné uspořádání stavebních částic

monokrystaly – mají pravidelné uspořádání v celém krystalu

(NaCl, CaCO3, SiO2)

 

polykrystaly – obsahují nahodile uspořádaná zrna, která jsou uvnitř pravidelně uspořádána. (zemina, prach, kovy), jsou izotropní

 

b) amorfní – beztvaré (asfalt, vosk, sklo, kaučuk)

polymery – bílkoviny, org. původ

 

izotropie- ve všech směrech má látka stejné vlastnosti (polykrystalické látky)

anizotropie – nejsou stejné vlastnosti (monokrystalické látky)

 

 geometrická mřížka – soustava rovnoběžek v prostoru, rozdělí krystal na soustavu rovnoběžnostěnů

ideální geometrická mřížka je mřížka pravidelně obsazená částicemi

– podle tvarů rovnoběžnostěnů rozlišujeme tzv. krystalografické soustavy – soustava krychlová (kubická) – elementární (základní) buňka je krychle

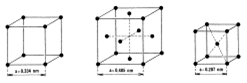
1) primární 2) plošně centrovaná 3) prostorově centrovaná

Vrcholy                 středy stran              střed krychle

–          Částice kmitají kolem bodů kryst. mřížky.

 

mřížkový parametr a- délka hrany krychle

 

Poruchy (defekty) krystalové mřížky

– v reálném krystalu existuje mnoho poruch od pravidelného uspořádání částic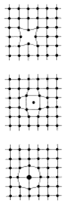

 

a) vakance – vzniká neobsazením rovnovážné polohy kryst. mřížky

příčina- tepelný kmitavý pohyb částic -> částice opustí své místo a vzniká neobsazené místo

dostaneme ozářením krystalu – elektrony, neutrony, ionty

 

b) intersticiální poloha – částice se nachází mimo pravidelný bod krystalické mřížky (v mezeře – )

 

c) příměsy (nečistota)

– cizí částice se vyskytuje v krystalu daného chem. složení

– nachází se buď v intersticiální poloze (podle počtu částic C v Fe dostaneme různé druhy oceli) nebo nahrazuje vlastní částici mřížky (polovodiče typu P nebo N – příměsi do struktury křemíku)

 

Typy vazeb

Síly které působí mezi částicemi v krystalické mřížce:

1.    Iontová – mřížku drží pohromadě elektrické přitažlivé síly mezi kationty a anionty

2.    Kovová – odpudivé elektrické síly kationtů kovu nepustí atomy na novou polohu, elektrony tvoří elektronový plyn mezi kationty – jsou volné

3.    Kovalentní – je to chemická vazba mezi atomy, kdy atomy mají společné valenční elektrony; je u izolantů nebo polovodičů (Si, Ge)

4.    Molekulová – síly mezi molekulami – je velmi slabá

 

Deformace pevného tělesa

 

tvárná (plastická) – přestaneme-li působit silou, deformace zůstává

pružná (elastická) – vrací se do původního tvaru, je dočasná

 

deformace tělesa = změna tvaru, objemu i rozměrů působením vnější síly

 

a) deformace tahem

 

F = -F

– roztahování – výtah jeřáb

 

b) deformace tlakem 

F = -F

– stlačování – pilíře, nosníky

 

c) deformace ohybem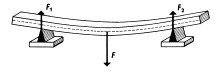

F – síla, působící vahou toho tělesa

 

– horní vrstva se deformuje tlakem

– spodní vrstva se deformuje tlakem

– prostřední část zůstává nezměněna

 

d) deformace smykem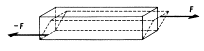

– posunutí vrstev, vzdálenost vrstev se nemění (šroub, nýt)

 

e) deformace kroucením – obsahuje 2 soustavy sil, vrták při vrtání, šrouby při utahování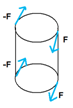

 

Síla pružnosti, normálové napětí

– tahové síly vyvolávající sílu F

– při deformaci nastává tzv. stav napjatosti, který je charakterizován normálovým napětím – Sigma n [Pa]

 

   síla pružnosti, která působí na příčný řez o obsahu S/ obsah plochy (v tab u Hoodova zákona na konci F / S)

 

(Fp = m g)

 

– ve stavu rovnováhy : F = -F

 

mez pevnosti – s_p, s_p < Sigma n ==>   poruší se soudržnost (přetrhnutí)

→ tab. str. 139

– křehké látky mají mez pevnosti blízko meze pružnosti (sklo)

mez pružnosti (elasticity) – s_E – max. hodnota Sigma n, kdy zůstává deformace pružná (pak už trvalá)

dovolené napětí – s_D – max. hodnota Sigma n, kdy při deformaci (tahem, tlakem) jde o pružnou deformaci. Podíl meze pevnosti a dovoleného napětí je součinitel (koeficient) bezpečnosti.

 

Př.:

d=?

m = 2,5t

Sigma n = 60 MPa

Sigma n = mg / pi d² / 4

d² = 4 mg / pi Sigma n = 2,3 cm

 

 

Př.: SIgma n = ? [Pa]

F = 0,25 kN

d = 2,1mm

Sigma n = Fp / s

 

Př.:

d = 15mm = 0,015m

(tyčinka)

F = 1,63 * 10⁵ N….. síla potřebná k jejímu přetržení

 

Urči mez pevnosti v tahu.

Sigma n = Fp / S

Sigma n = 163000 / pi r² = 163000 / 0,000176625 = 922 859 165 Pa

 

Hookův zákon pro pružnou deformaci tahem

– vyjadřujeme závislost normálového napětí s_n a relativního prodloužení epsilon ε

Sigma n = Fp / s

v tab je, ale není popsát jako ε =!!!

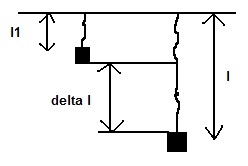
delta l = l – l1 (konečná délka – počáteční délka)

 

=> prodloužení vůči původní délce. Pokud chceme v procentech, tak ε * 100

 

Hookův zákon zní: normálové napětí je přímo úměrné relativnímu prodloužení:

 

Sigma n = E * ε

 

E… modul pružnosti v tahu (konstanta charakterizuje látku)

 

– hookův zákon platí pouze pro pružnou deformaci tahem

– je-li E malé, normálové napětí se mění pomalu

ε = 1… prodloužení o vlastní délku

 

Graf relativního prodloužení:

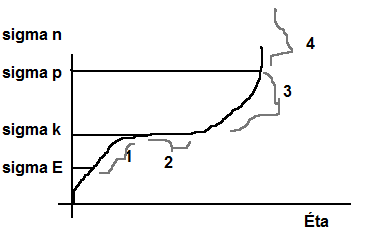
sigma K – mez kluzu

 

1 – dopružení

2 – látka teče

3 – zpevnění materiálu

4 – roztržení materiálu

 

– různé materiály mají různé délky částí

 

Délková, objemová roztažnost

V = V1 [1 + Beta (t – t1)]

– u délkové roztažnosti místo V1 je l1, místo beta je alpha, místo V je l

Beta… součinitel objemové roztažnosti

Aplha… … součinitel délkové roztažnosti

 

 

př.: Ocelový drát má při t2=-15C délku 1000m. Urči jeho délku při teplotě 45C

alpha = 11,5 * 10⁻⁶ K

l – 1000 * [1 + 11,5 * 10⁻⁶ * 60]

l = 1000 * [1 + 690 * 10⁻⁶]

l = 1000 * [1,00069] = 1000,7 m

 

př.: t1 = 20C

V1 = 1 l

delta V = ?

t = 80C

 

1l = dm³ = 0,001 m³

Beta = 2,4 * 10⁻⁵ K⁻¹

 

V = 0,001 [1 + 2,4 * 10⁻⁵ (60)]

V = 0,001 * 1,00144

V = 0,00100144 m³

 

deltaV = 0,001 – 0,00100144

deltaV = 0,00000144 m³

deltaV = 1,44 cm³

 

Proces tání

– změna skupenství pevného na kapalné

– většina pevných látek procesem tání zvětšuje svůj objem

– výjimky: led, bismut, germanium – ty táním svůj objem zmenšují

 

Podmínky uskutečnění tání

a) dosažení teploty tání t_t (různá, souvisí s vnějším tlakem)

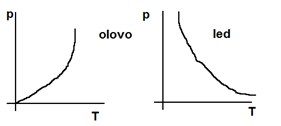
– u ledu se zvyšující teplotou tlak snižuje -> regulace ledu

 

b) musíme dodávat teplo, než těleso roztaje -> skupenské teplo tání L_t [J] = teplo, které musíme dodat tělesu, zahřátému na teplotu tání L_t, aby se roztálo

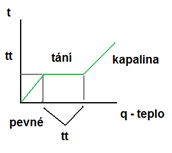
Q = m c delta t

c… měrná tepelná kapacita

 

 

př.: Q = ? [J]

m = 10 kg

t1 = 20 C

tt = 660 C

c = 896 J kg⁻¹ K⁻¹

lt = 400 K J kg⁻¹

 

Q1 = m c delta t

Lt = m lt

 

Q = Q1 + Lt

Q = 10 * 896 * 640 + 10 * 400 000

Q = 57344 * 10² + 4 * 10⁶

Q = 94 344

 

Př.:

ε = 62% = 0,62

M = 5 t = 5 * 10³ kg

E = ?

T1 = 16 C

Tt = 1300 C

C = 460 J kg⁻¹ K⁻¹

Lt = 82 kJ kg⁻¹ = 82 * 10³ J kg⁻¹ K⁻¹

 

ε = Q / E

Q = m c (t1 – 1) + m * lt

Q = 5 * 10³ * 460 * (1300 – 16) + 5 * 10³ * 82 * 10³

Q = 5 * 10⁴ * 46 * (1284) + 5 * 10⁶ * 82

Q = 23 * 10⁵ * 1284 + 41 * 10⁷

Q = 29532 * 10⁵ + 41 * 10⁷ = 33632 * 1-^5 J

 

 

Vypařování (koncenzace)

– přeměna kapaliny na plyn

–          Probíhá za každé teploty

Urychlíme:

–          Zvýšením teploty

–          Odvodem par

–          Zvětšení plochy

 

–          Skupenské teplo vypařování (varu) – Lv

–          Množství tepla, které musíme dodat, aby se látka změnila v páru téže teploty.

– měrné skupenské teplo vypařování (také Lv)

Lv = Lv / m [J Kg⁻¹]

 

–          Lv s rostoucí teplotou klesá

 

Př.: voda  0C à l_v = 2,51 MJ kg⁻¹           … tab. 152

100C à l_v = 2,26 MJ kg⁻¹

 

Var – proces, kdy k vypařování dochází v celém objemu kapaliny (vypařování odevšud)

–          Bublinky páry vznikají uvnitř kapaliny

–          Je podmíněn teplotou varu

 

Např.: H2O při normál. atmosférickém tlaku 101 kPa má teplotu varu 100 C

–          Teplota varu závisí na vnějším tlaku

–          S rostoucím tlakem teplota varu roste, se snižujícím klesá

–          Využití: v tlakových nádobách – papinův hrnec

 

 

Sublimace

–          Proces, při kterém se pevná látka přímo mění na plyn

–          Sublimuje např.: sníh, led, jód, kafr, naftalen, ale i vonící a páchnoucí pevné látky

–          Měrné skupenské teplo sublimace ls = Ls / m

–          Ls závisí na teplotě, kdy látka sublimuje

 

Desublimace

–          Přeměna látky z plynného stavu na pevné. Např. jinovatka, kdy vodní pára nesublimuje na pevné krystalky při teplotách menších, než 0C

 

Sytá pára

–          Vzniká v uzavřené nádobě

–          Prostor nad kapalinou se zasytí (obsahuje maximální možný počet molekul plynu)

–          V uzavřené nádobě dochází k dynamické rovnováze à objem syté páry a kapaliny je stejný

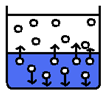
Vlastnosti syté páry

–          Je v rovnováze s kapalinou

–          Neplatí Van der Walsova rovnice ani stavová rovnice (p * V / T – není konstantní)

–          Tlak syté páry se při konstantní teplotě nemění s objemem

–          Při rostoucí teplotě se tlak syté páry zvyšuje

–          Tlak syté páry závisí pouze na chemickém složení

 

Vlhkost vzduchu

Absolutní vlhkost:

Ф = m / V

– udává hmotnost páry v určitém objemu.

 

Relativní vlhkost:

fí = Ф / Ф_m

 

Podíl absolutní vlhkosti / vlhkostí, kdy je vodní pára ve vzduchu sytou parou

 

A….trojný bod à je to stav, kdy pevná látka, kapalina i plynná látka jsou v dynamické rovnováze

K … kritický bod à je to poslední bod křivky, ve kterém jde určit, zda se jedná o plynnou látku nebo kapalinu