Hydrostatika a proudění tekutin

Vztlaková síla v kapalinách a plynech

– Tělesa ponořená do kapaliny jsou lehčí, než ve vzduchu

– Nadlehčuje je vztlaková síla F_vz, směřující vzhůru, která je důsledkem hydrostatického tlaku kapaliny

 

Ponoříme-li do kapaliny kvádr, působí na každou jeho stěnu kolmá tlaková síla. Síly, které působí na boční stěny se navzájem vyruší, na horní stěnu působí síly F₁ = p_h1 × S a na spodní F₂ = p_h2 × S.

Jejich výslednice je vztlaková síla

 

F_VZ = F2 – F1 = r * S * h₂ * g –  r * S * h₁ * g = r S * h * g = r V * g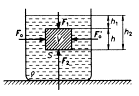

V = S × h je objem kvádru.

Archimédův zákon:

 

Důsledkem Archimédova zákona je různé chování těles v kapalině:

 

– Na každé těleso ponořené do kapaliny totiž proti vztlakové síle působí ještě Země tíhovou silou

   F_G = ρ_t × V × g  ve svislém směru dolů…… r_t je průměrná hustota tělesa

výslednice F = |FG – Fvz|

 

Mohou nastat 3 případy:

1) r_t > r_k Þ F_G > F_vz  -> výslednice sil F směřuje dolů a těleso klesá ke dnu (kovové předměty ve vodě)

2) r_t = r_k Þ F_G = F_vz  -> výslednice sil F = 0 a těleso se v kapalině vznáší (ryby a mořští živočichové)

3) r_t < r_k Þ F_G < F_vz  -> výslednice sil F směřuje nahoru a těleso stoupá k volné hladině kapaliny. Po dosažení hladiny nadskočí a poté se ustálí v takové poloze, že tíhová síla F_G je v rovnováze se vztlakovou silou  jejíž velikost se rovná tíze kapaliny stejného objemu V‘, jakou vytlačuje ponořená část tělesa.(dřevěný špalek ve vodě).

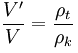
ρ_k – hust. Kapaliny, V‘ objem  ponořené části,  není v tab.

-> Těleso se ponoří do kapaliny tím větší částí svého objemu, čím je jeho hustota větší, nebo čím je hustota kapaliny menší. Tohoto poznatku využívají hustoměry (slouží k měření hustoty kapalin).

 

Vztlaková síla plynů

Vztlakovou silou působí nejen kapaliny, ale také plyny, nadlehčována jsou i všechna tělesa ve vzduchu, však mnohem menší silou, kvůli malé hustotě plynů. Při vážení předmětů, které mají hustotu mnohem větší než plyny lze vztlakovou sílu zanedbat, ale existuje.

 

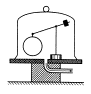
Když na vzduchu vyvážíme skleněnou baňku a poté vývěvou odčerpáme vzduch, klesne baňka, protože ve skutečnosti je těžší. Když pod zvon opět pustíme vzduch, baňka a závaží budou opět v rovnováze.

Na principu vztlakové síly vzduchu fungují balóny a vzducholodě (teplý vzduch a vodík nebo helium je lehčí než studený vzduch).

Proudění kapalin a plynů

 = takový pohyb tekutin, kdy u částic převažuje pohyb v jednom směru. (voda v řekách, voda a plyn v potrubí)

– složitější, než pohyb pevných látek, protože jednotlivé částice mohou měnit vzájemnou polohu

– Pokud je rychlost v částic stálá, jde o ustálené (nejjednodušší, každým průřezem kapaliny protéká stejný objem)

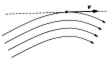Trajektorie jednotlivých částic proudící tekutiny znázorňujeme proudnicemi. Proudnice je myšlená čára, jejíž tečna v libovolném bodě má směr rychlosti v pohybující se částice. Každým bodem proudící tekutiny prochází při ustáleném proudění jen jedna proudnice Þ proudnice se nemohou navzájem protínat.

Proudové vlákno je průřez trubice, kterou proudí kapalina; plocha, kterou proudí kapalina.

 

Objemový průtok

= objem kapaliny, který proteče daným průřezem trubice za jednotku času

Q_V = S × v  [m³/s] … průřez o obsahu s a rychlost kapaliny, není v tab!

Qv = V / t

 

Rovnice kontinuity

Ideální kapalina je nestlačitelná, proto se na žádném místě nemůže hromadit, proto je objemový průtok v každém průřezu stejný. Q_V = konst.

V místě, kde se zúží průřez trubice, se zvětší rychlost proudění. (Na zahradě, když chceme dostříknout dál –přiškrtíme hadici).

 

 

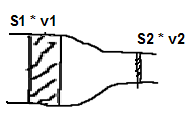
S1 * v1  =  S2 * v2            = S * v                                                   (­S2 < S1, v1 > v1)

Q_V1 = Q_V2

 

Pro plyny:

U plynů jejich hustota závisí na míře stlačení  musíme započíst i hustotu:

Hmotnostní průtok Q_m = hmotnost látky, která projde průřezem trubice za jednotku času.

Q_m = r × Q_V  [kg / s] – není v tab.

Rovnice kontinuity plynů:  ρ₁ × S₁ × ρ₁ = ρ₂ × S₂ × v₂ = ρ × S × v = konst.

 

Objem vody, který potrubím proteče za libovolnou dobu měříme vodoměrem, objem plynu plynoměrem.

 

Proudění reálné kapaliny způsobuje tření a rychlost pohybu částic není konstantní. To se projevuje při vysokých rychlostech víry → turbulentní proudění. Pro překonání odporu kapaliny se žene potrubím pomocí čerpadel → zvýšení tlaku.

 

 

Př :

v = 3m / s

S = 80 m³

Qv = S v = 3 * 80 = 240 m³/s

 

Př :

v = 0,5 m/s

S = 30 cm² = 0,003 m²

Qv =  0,5 * 0,003 = 0,0015 m³/s ( = 1,5 l/s )

 

Př :

Potrubím o obsahu kolmého řezu 50 cm² proteče za dobu 5 minut 5000 litrů vody.

a) Objemový průtok vody

S = 50 cm²

t = 5 min = 300 s

V = 1500 l = 1500 dm³ = 1,5 m³

Qv = ?

Qv = 1,5 / 300 = 0,005 m³/s = 5 l/s

 

b) Velikost rychlosti proudící vody

Qv = S v

v = Qv / s

v = 0,005 / 0,005 = 1

 

Př :

S1 = 120 cm² = 0,012 m²

S2 = 20 cm² = 0,002 m²

V1 = 0,5 m/s

V2 = ?

 

S1 v1 = S2 v2     

v2 =  S1 v1 / S2

 

v2 = 0,012 * 0,5 / 0,002

v2 = 3 m/s

 

 

 

Bernoulliho rovnice

Bernoulliho rovnice vyjadřuje zákon zachování mechanické energie (Ek + Ep = konst.) pro proudění ideální kapaliny ve vodorovném potrubí: Když se ve zúženém místě zvětší rychlost kapaliny, získá větší kinetickou energii. Podle ZZE se musí přeměnit z energie potencionální.

Trubice je vodorovná -> nejde o potenciální energii tíhovou

Kapalina je nestlačitelná -> nejde o potenciální energii pružnosti

Jde o potenciální tlakovou energii

 

Velikost tlakové potenciální síly určíme z práce, kterou vykoná tlaková síla F působením na píst o průřezu S a délce l.

Kinetická energie:

Podle zákona zachování energie platí:

 

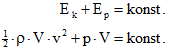
Po vydělení rovnice objemem V:

 

Součet kinetické a tlakové potenciální energie kapaliny o jednotkovém objemu je ve všech částech vodorovné trubice stejný.

 

 

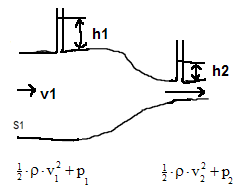
Ek1 + Ep1 = Ek2 + Ep2

 

V místě většího průřezu a menší rychlosti je větší tlak

 

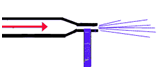Při velkém zúžení trubice nabývá rychlost velkých hodnot a tlak klesne až pod hodnotu atmosférického tlaku. V zúženém místě vzniká podtlak (hydrodynamický paradoxon) – využití u vodní vývěvy (nasává se vzduch). Podtlak vzniká i u plynů (rozprašovače, stříkací pistole, karburátor).

 

 

Výtoková rychlost

– také ze zákona zachování mech. energie: Ek = Ep

Ep = mgh = ró g h V

1/2 ró V v² = ró g h V…. v = sqrt(2 g h)

 

 

Obtékání těles reálnou tekutinou

obtékání = těleso se pohybuje vzhledem k tekutině, ve které je ponořené

– mezi tělesem a tekutinou působí tření => hydrodynamická (u kapalin) a aerodynamická (u plynů) odporová síla -> odpor prostředí.

 

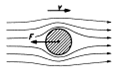Při malých rychlostech je proudění kolem těles laminární (vrstevnaté – jednotlivé proudnice, vrstvy se nemíchají) a odporová síla F je poměrně malá a roste přímo úměrně relativní rychlosti v (tělesa vzhledem k prostředí).

 

Při větších rychlostech vzniká proudění turbulentní, velikost odporové síly F se zvětšuje už s druhou mocninou rychlosti v. Pro velikost aerodynamické odporové síly odvodil Newton vztah

,

kde C je součinitel odporu pro daný tvar tělesa, r hustota plynu, S obsah průřezu tělesa kolmého ke směru pohybu av relativní rychlost.

Newtonův vztah platí pro středně velké rychlosti. Pro nadzvukové rychlosti je odporová síla úměrná třetí mocnině rychlosti v. Těleso vytváří rázovou vlnu – rány při přeletu nadzvukových letadel.

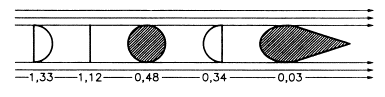 – není v tab., stačí znát které jsou větší/menší

Největší odpor má dutá polokoule (padáky), nejmenší těleso proudnicového neboli aerodynamického tvaru (ptáci, ryby, letadla, závodní auta)

 

Křídla malých letadel jsou aerodynamického tvaru a nesouměrná – horní plocha je větší než spodní, vzduch ji obtéká rychleji. Podle Bernoulliho rovnice je větší tlak na spodní plochu křídla a na celou nosnou plochu křídla pak působí vztlaková aerodynamická síla F_y. Dále na křídlo působí ještě odporová síla F_x, kterou překonává tah motorů. Jejich výslednicí je výsledná aerodynamická síla F = Fx + Fy.

­Fy     F

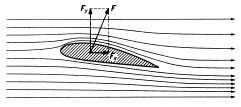Fx

 

Pascalův zákon a využití v hydraulických zařízeních

 – viz otázka číslo 5

 

 

 

Tlak v kapalinách vyvolaný tíhovou silou

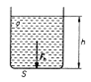 – hydrostatická tlaková síla F_h je vyvolána působením tíhové síly Země a působí na dno nádoby nebo na ponorky, potápěče…

 

F_h = F_G = m × g = ρ × S × h × g                                    ; V = S × h; m = ró V

S… obsah dna nádoby

 – závisí na hustotě kapaliny, na obsahu dna a na hloubce pod volným povrchem kapaliny.

 

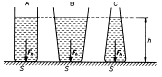Nezávisí na tvaru a celkovém objemu kapalného tělesa.

hydrostatický paradoxon = v nádobách jiného tvaru se stejnou výškou hladin a stejným obsahem dna je tlak na dno stejný.

 

 

 

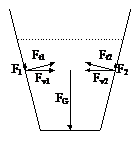Důvod:  na dno působí tíhová síla F_G. Kapalina zároveň působí kolmými tlakovými silami na stěny. Reakce kolmých sil působí na kapalinu. Tyto reakce jsou síly F_t1 a F_t2. Rozkládají se na svislé složky F₁ a F₂ a vodorovné F_v1 a F_v2. Vodorovné složky se vzájemně zruší a svislé nadlehčí kapalinu právě tak, že na dno působí je síla F_h, přestože velikost F_G je v tomto případě větší.

 

 

Tlak v kapalině vyvolaný hydrostatickou talkovou silou se nazývá hydrostatický tlak p_h.

 

Hydrostatický tlak je přímo úměrný hustotě kapaliny a hloubce místa pod volným povrchem kapaliny.

Místa o stejném hydrostatickém tlaku se nazývají hladiny.

volná hladina  = hladina o nulovém hydrostatickém tlaku je na volném povrchu kapaliny.

 

Spojené nádoby

– lze vysvětlit hydrostatickým tlakem a Pascalovým zákonem

– u dna spojeny trubicí, tvar může být jakýkoli.

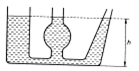Nalijeme-li do těchto nádob kapalinu o stejné hustotě, pak se hladina ve všech nádobách ustálí ve stejné výšce h nad společným dnem. Je to způsobeno důsledkem Pascalova zákona – ve všech místech kapaliny je stejný tlak. U dna tedy bude tlak p_h = r × h × g. r a g jsou stejné, proto musí být i stejná výška h.

 

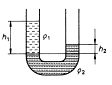Z toho, že princip spojených nádob vychází z Pascalova zákona, můžeme odvodit i to, že ve spojených nádobách, ve kterých jsou různé kapaliny, jsou hustoty kapalin v převráceném poměru k výškám kapalin nad společným rozhraním, protože tam je hydrostatický tlak stejný.

 

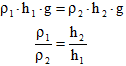
Tlak vzduchu vyvolaný tíhovou silou

Tíha atmosféry, která působí kolmo k dané rovině, se nazývá atmosférická tlaková síla F_a. Působí na všechna tělesa i na celý povrch Země. Tlak jí vyvolaný se nazývá atmosférický tlak p_a.

 

Normální atmosférický tlak u hladiny moře je 101,325 kPa. Každých 100 m do výšky se zmenší asi o 1,3 kPa.

– tloušťku atmosféry nelze spočítat, protože hustota vzduchu není stálá.

 

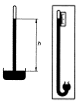Tlak vzduchu se měří barometry. Rtuťový barometr objevil Torricelli – tvoří ho trubice, která má zatavený jeden konec. Použil rtuť – má větší hustotu, protože s vodou by měl sloupec 10 metrů – všiml si, že nevyčerpá pumpou vodu výš, než do 10m. Když ji naplníme rtutí a otočenou ponoříme do nádobky tak, aby rtuť nevytekla – na rtuť tlačí atmosférický tlak, proto nevyteče. Výška rtuťového sloupce se ustálí ve výšce h, při níž je hydrostatický tlak rtuti stejný jako atmosférický tlak.

Podle výšky hladiny lze určit tlak vzduchu (→ jednotka Torr = mm Hg; normální tlak – 760 mm Hg).

Normální tlak určený rtutí: P_n = h × r × g = 0,76 × 13595,1 × 9,80665 = 101325 Pa

 

Běžnější, ale méně přesný barometr je kovový – aneroid. Pro průběžné zaznamenávání tlaku se používá barograf.

Atmosférický tlak se mění a tyto změny provází změny počasí – při vysokém tlaku bývá jasno, sucho; při nízkém zataženo, vlhký vzduch, často prší.

 

U kapalin je někdy důležitý tzv. absolutní tlak – vzhledem k tlaku vakua 0 Pa. Většina tlaků, které se v praxi měří, jsou přetlaky nebo podtlaky a měří se rozdíl od jiného tlaku, většinou atmosférického. Lze tak vysvětlit, proč má potápěč v hloubce 10 m pod hladinou v plicích polovinu objemu vzduchu oproti tomu, kdy byl na hladině. Je to proto, že na něj působí hydrostatický tlak vody (v 10 m asi 10⁵ Pa) a navíc atmosférický tlak (asi 10⁵ Pa). Celkový tlak na něj působící je 2 × 10⁵ Pa. Stejně tak když v pneumatice změříme tlak kolem 3 × 10⁵ Pa, absolutní tlak, který bychom změřili vzhledem k tlaku vakua (0 Pa) je 4 × 10⁵ Pa.

 

Podtlak se také využívá pro čerpání vody ze studny. Když odpustíme vodu, snaží se atmosférický tlak vyrovnat vzniklý podtlak a tím se načerpá další voda. Ze studny lze ručně nebo jedním čerpadlem získat vodu maximálně z deseti metrů (v této výšce už jen samotný vodní sloupec vyvolá tlak, který je roven atmosférickému, proto už nevznikne dole ve studni podtlak přes veškerou snahu).