Mechanické kmitání a vlnění

Mechanické kmitání

 

Kmitavý pohyb – těleso nebo hmotný bod se pohybuje po úsečce nebo kruhovém oblouku kolem rovnovážné polohy.

 

Periodický kmitavý pohyb – rovnovážnou polohou prochází v pravidelných časových intervalech (těleso zavěšené na pružině, písty v motoru)

 

Rovnovážná poloha = taková poloha, kde má těleso nejmenší potenciální energii. Po skončení pohybu těleso zůstává v rovnovážné poloze, dokud na něj nezačne působit vnější síla.

 

Mechanický oscilátor

= zařízení, které kmitá bez vnějšího působení

= závaží zavěšené na pružině, ustalující se hladina nebo kyvadlo.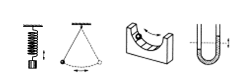

Podobně kmitá i kyvadlo = těleso zavěšené nad těžištěm, které kmitá kolem své rovnovážné polohy po kruhovém oblouku, jehož středem je osa, která prochází závěsem. Mat. kyvadlo – zanedbává váhu závaží, deformaci provázku a odpor prostředí. (kreslit)

 

Kinematika kmitavého pohybu

perioda T [s] = čas, po kterém se periodický pohyb opakuje

frekvence (kmitočet) pohybu = počet opakování za jednotku času.

   [f] = s^–1 = Hz (hertz), v tab u mechaniky.

Nejjednodušší kmitavý pohyb je harmonický pohyb = okamžitá výchylka z rovnovážné polohy je závislá na funkci sinus, grafem je sinusoida.

Harmonický kmitavý pohyb je pravoúhlý průmět rovnoměrného pohybu po kružnici. Rovnovážná poloha je ve středu kružnice.

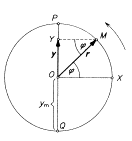Při pohybu mechanického oscilátoru se okamžitá výchylka y periodicky mění a vzhledem k rovnovážné poloze nabývá kladných i záporných hodnot. V určitých časech dosahuje y největší kladné, popř. záporné hodnoty. Absolutní hodnota největší výchylky je amplituda výchylky y_m.

 

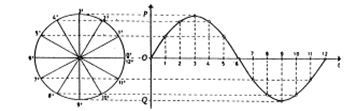
Když necháme obíhat hmotný bod po obvodu kružnice, jejíž střed umístíme do počátku soustavy souřadnic, jeho polohu popisuje vektor r, který má počáteční bod ve středu kružnice a koncový v hmotném bodě. Okamžitá výchylka y je pak průmět vektoru r do osy y.

 

Úhel φ ([φ] = rad) se nazývá fáze kmitavého pohybu:

 

ω je úhlová frekvence. Je to úhel, který hmotný bod urazí za jednotku času.

[ω] = rad × s^–1

Pro okamžitou výchylku platí vztah:

Popisuje okamžitou výchylku kmitavého pohybu tělesa, které se v počátečním okamžiku nachází v rovnovážné poloze. Když M leží na ose x:  r = y_m.

 

Rychlost a zrychlení harmonického pohybu

Rychlost harmonického pohybu je změna výchylky za čas

– největší v rovnovážné poloze, v amplitudě nulová.

Největší rychlost harmonického pohybu je amplituda rychlostí v_m = ω × y_m

 

Zrychlení harmonického pohybuj je změna rychlosti za čas

 

Zrychlení harmonického pohybu směřuje proti výchylce, největší je v amplitudě, nulové v rovnovážné poloze. Zrychlení harmonického pohybu je přímo úměrné okamžité výchylce a v každém okamžiku má opačný směr. Největší zrychlení harmonického pohybu je amplituda zrychlení a_m = ω² × y_m

 

Přeměny energie v mech. oscilátoru

U kmitání dochází k period. přeměnám energie. Celková energie mechanického oscilátoru se skládá z:

Kinetické energie:

 – tab v mechanice

Tíhové potenciální energie:

E_p = m × g × h

Potenciální energie pružnosti je

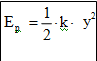  – není v tab!

podobná kin. energii,jen k je tuhost pružiny, y (delta l) je výchylka z rov. Polohy (prodloužení)

Klidová energie oscilátoru je

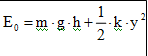 – není v tab!

Když těleso oscilátoru prochází rovnovážnou polohou: (nejv. rychlost i energie)

            – není v tab!

 

v = ω * y_m, potenciální energi pružnosti je nulová

 

Když těleso dosáhne amplitudy y_m (krajní poloha), je jeho kinetická energie nulová a potencionální pružnosti maximální:

           – není v tab!

 

Při harmonickém pohybu se periodicky mění potenciální energie kmitání v energii kinetickou a naopak. Celková energie oscilátoru je konstantní a je rovna součtu klidové energie oscilátoru energie kmitání dodané oscilátoru při uvedení do kmitavého pohybu.

 

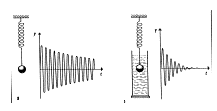Na oscilátor ve skutečnosti působí odpor prostředí, i když se s ním ve výpočtech neuvažuje. Amplituda se postupně zmenšuje, až je nakonec nulová. Energie se mění na jiné formy než mechanickou – většinou na vnitřní energii → ohřeje oscilátor a prostředí). Kmitání, u kterého se zmenšuje amplituda, se nazývá tlumené kmitání.

Na míru tlumení má vliv prostředí. Při kmitání ve vzduchu se amplituda výchylky zmenšuje velmi pomalu, ve vodě rychleji. Kdyby oscilátor kmital v medu, neudělal by ani jednu periodu.

 

Vlastní kmitání oscilátoru je vždy tlumené. Abychom získali netlumené kmity, musíme na oscilátor působit silou, aby se kmity netlumily. Takové kmity se nazývají nucené kmitání mech. oscilátoru. Při nuceném kmitání oscilátor kmitá vždy s frekvencí vnějšího působení. Nucené kmitání vzniká působením periodické síly na oscilátory i na objekty, které vlastnosti oscilátoru nemají. Frekvence nuceného kmitání závisí na frekvenci působící síly a nezávisí na vlastnostech kmitajícího objektu. Nucené kmitání je netlumené.

 

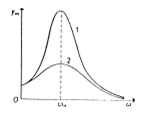Rezonance – frekvence nutící síly se přiblíží vlastní frekvenci oscilátoru, velmi se zvětší amplituda kmitů. Měníme-li frekvenci nutící síly, pak v hodnotě frekvence vlastních kmitů je amplituda největší – vznikne maximum. Maximum je tím ostřejší, čím méně se tlumí vlastní kmity. Graf závislosti amplitudy nucených kmitů na frekvenci nutících kmitů je rezonanční křivka. Rezonanční frekvence se poněkud zmenšuje s rostoucím tlumením.

Význam rezonance spočívá v tom, že umožňuje rezonanční zesílení kmitů. Malou, periodicky působící sílou lze v oscilátoru vzbudit kmitání o značné amplitudě výchylky, pokud je perioda vnějšího působení shodná s periodou vlastního kmitání oscilátoru.

Rezonance je využita např. u hudebních nástrojů.